How many times have you seen a TV talk show mention how someone failed a polygraph, so they must have cheated! Lie detectors don’t lie, right? How many times have you had a friend get bad news on a medical test and see that emotional toll that took on them?
What could these two have in common? They could both be helped by Bayes’ theorem.
Bayes’ theorem is an idea in statistics that allows us to update the probability of something happening based on new evidence. You can see what it looks like in the featured image above. However, the best explanation I have ever seen comes from this image:
Let’s go through each part of this image individually:
- H: This is our hypothesis, or what we think is true. In the talk show example, this could be “I think my man is cheating on me.”
- D: This is our new information. For the talk show, it’d be the results of our polygraph test.
- P(H|D): This is the likelihood that the hypothesis is true given our new information. “What are the odds that my man is lying about cheating on me if the polygraph says he’s a liar?”
- P(D|H): This is the odds of seeing the new information if the hypothesis is true. Here, it’d be the odds that the polygraph would say someone was lying when they were lying. This turns out to be 88% (Rice, 2007).
- P(H): This was the probability that the hypothesis was true before the new information. For example, 22% of men say that they have cheated on a significant other.
- P(D): This the odds of the test saying the person was lying in every outcome. Here, you’d use the 88% it says someone is lying when they are, and multiply the odds that your man is lying (22%). You’d also have to add the odds the test says they are lying when they are not (false positive), about 14% (Rice, 2007), multiplied by the 78% chance your man isn’t a cheater.
This gives us the following result:
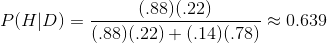 ,
,
or 63.9%. This means that less than two out of three of those polygraph results are actually accurate. This low success rate, by the way, is one of the reasons most states don’t allow polygraphs in court.
But what about the bad medical test? How could it help us there? In statistics circles, the common example is the case of mammogram result that comes back positive for cancer. For our purposes, we’ll use numbers used by The New Yorker when they talked about this problem in this article from 2013. The numbers they quote are as follows:
- The chances that a women in her forties has breast cancer is 1.4% (meaning 98.6% don’t).
- The chances that a mammogram comes back positive when the woman has cancer is 75%.
- The chances that the mammogram comes back positive when the woman doesn’t have cancer is 10%.
Let’s imagine your friend in her 40s gets a positive result back on a mammogram. What are the odds that she actually has cancer? Bayes’ theorem tells us the probability would be
 ,
,
or only 9.6%. If that seems low to you, don’t worry: one study showed that 95% of physicians given similar numbers incorrectly estimated the likelihood to be about 75% (Rice, 2007). Your friend should be concerned and have further work done, but you can comfort her by saying that there is an over 90% chance it is a false positive for her.
What can Bayes’ do for you? It can help make talk shows more laughable, and it can help bring comfort when tests go south. It helps to give perspective and a more realistic view of the world. As it turns out, it’s pretty useful.
We’ll continue to explore these ideas in movie night this week with some videos that give even more examples about how Bayes’ theorem can help you every day.
The odds that those will be entertaining? 100%.



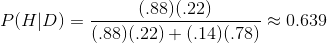 ,
, ,
,