Cones in Space!

In geometry, there are a group of shapes called the conic sections: the circle, the ellipse, the parabola, and the hyperbola. Why are they called conic? It’s because each can be generated by cutting a cone a certain way:

Figure 1: Source

It sometimes comes as a surprise to students why so much emphasis is placed on these shapes. Of all the curves that can be made, why spend so much time discussing and learning about four of them?

Honestly, it’s because these shapes have a large number of applications for the world in which we live, and I’ll be returning to a few in my upcoming posts. However, one use of conic section is literally how the world goes ’round. Conic sections are seen with nearly every object in space to some degree, because conic sections are the shapes of orbits.

Figure 2: Circular orbit: yellow, Elliptical orbits: red, Parabolic trajectory: blue, Hyperbolic trajectory: green. Source

Circular Orbits

A circular orbit is a type of orbit where the orbiting body (like a moon or satellite) is always the same distance from the body it is orbiting  (such as a star or planet). Despite them being the most popular orbits to show in many pictures of orbits, there aren’t any completely circular orbits in real-life. To have a perfectly circular orbit, the velocity of the object has to be exactly  right, and there is always a small degree of error. However, one example that comes close to being completely circular are geostationary satellites used for communications and weather satellites. It is important for satellites like these to always be above the same spot on Earth, and the only way to do this is to have a circular orbit directly on the equator. However, it takes fuel to maintain that circular orbit, so these satellites aren’t able to maintain these orbits indefinitely.

Elliptical Orbits

Basically everything that has an orbit has an elliptical orbit (shown in red in Figure 2). Without getting too far into the math, the body being orbited is found in one of the foci (pronounced foe’-sigh; the singular version would be focus).

Figure 3: Source

Every planet orbits the sun in an ellipse, which means that they move closer or further way at different times of year. For the eight major planets, this difference is very small. For the outer dwarf planets like Pluto and Eris, their orbits can be highly elliptical.

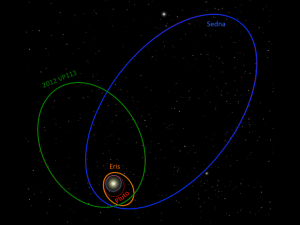
Figure 4: The orbits of a few outer dwarf planets. Source

The closer an object is to what it is orbiting, the faster it moves. The further away it is, the slower it moves. The Russians took advantage of this when solving a problem they had. The geostationary satellites that were mentioned when we talked about circular orbits? Their main downside is that they must be over the equator. This doesn’t work well for Russia in the Arctic Circle. As a result, they invented the Molniya orbit to help fix the problem. They put their communications satellites in a highly elliptical orbit so that they would be above Russia for 10 out of every 12 hours. This is just one example how these conic sections can help provide creative solutions to difficult problems.

Parabolic and Hyperbolic Trajectories

In order for something to escape the gravitational pull of a bigger body, it has to be moving fast enough. The minimum speed to escape is called the escape velocity. If an object moves at exactly the escape velocity, their trajectory will form a parabola (shown in blue in Figure 2). Like circular orbits, perfectly parabolic orbits do not truly exist, but most of our spacecraft will typically be as close to they can. Using the minimum amount of fuel to definitely escape is one of the main challenges to engineering. You don’t get to carry an extra can of rocket fuel with you into space, just in case! Naturally, most escape trajectories will be hyperbolic in nature (shown in green in Figure 2), which is when the speed is above the escape velocity.

The next time you look into the night sky and see the moon, or a planet, or even the stars, hopefully you’ll remember how powerful an understanding of the conic shapes are in being able to describe what you see. And maybe, just maybe, the next time your math teacher asks you to find the focus, focusing will not longer be an issue.